| Zeitschrift Umělec 2004/4 >> Three Sources and Three Parts of Geometrising Visions of Ladislav Daněk | Übersicht aller Ausgaben | ||||||||||||
|
|||||||||||||
Three Sources and Three Parts of Geometrising Visions of Ladislav DaněkZeitschrift Umělec 2004/401.04.2004 Jan Andres | profil | en cs |
|||||||||||||
|
Faculty of Science, Palacky University, Olomouc
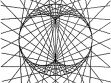
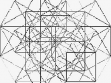
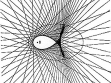
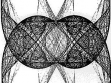
Ladislav Daněk (b.1958) is a reputable Olomouc artist and a respected art theoretician. Let us refer to more eligible ones as far as the basic characteristics of his work are concerned. The three following quotations reflect sufficiently the nature and un-interchangeability of Daněk´s hand: “Geometry, geometry, geometry. That is what Daněk´s drawing is. Hundreds of hours of austere drawing on construction graph paper whose regular rectangular raster provides a base for a new, differently structured geometrical network. However, even the maximal strictness in maintaining the geometrical build-up and mineralising of minor deviations caused by quivering of the hand sometimes brings a surprisingly lyrical sensation. Clumps of light and dark points invoke an illusion of volatile shivers which is illuminated by the inner light streaming out of his drawings. Impersonal drawing evoking a sensual experience – is this not a proof above all proofs that the artistic order of his style of work in itself has its own life with a wide range of possible messages?! As if the author were not a discoverer but a mere servant called up to mediate a message that has already been existing elsewhere. And he is the only one who knows where to look for it. The only one able to suppress various aestheticising artistic cravings and let this unique austere system speak its unexpectedly rich language.” (Radek Horáček in “Ladislav Daněk, Vladimír Havlík, Petr Jochmann, Inge Kosková” exhibition catalogue, Gallery Na Skořepce, Brno, 5 April – 3 May 1991.) “We perceive the resulting drawing not only as a field created by a diverse intensity of lines, knot points and interferences but also as a kind of oscillation or shivering, thickening and thinning, or as a dynamic surface ruled by its own regulations. ” Jiří Valoch in “Ladislav Daněk – Drawings” exhibition catalogue, Gallery Pod podloubím, Olomouc, 17 October – 5 November 1987.) “Ladislav Daněk has woven a colourful fluidity of hundreds of lines into a green warp of force field. Strenuously and persistently, he has looked for light resonating in the depths of infinity. He finds it in the harmony of strict geometrical order and in a dizzying effect of energy centers. By patient connecting and crossing of cosmic paths, he has drawn a way for an inattentive sight towards the mystical transcendency. ” (Yvonna Boháčová in “Forgotten Light” (Ladislav Daněk, Vladimír Havlík, Václav Stratil) exhibition catalogue, Sovinec (St. Augustin Church), 5 September – 28 October 1992.) The most distinctive effect of Daněk´s work is thus reached by creating non-linear structures (often resembling a negative picture), including dynamic and optical illusions, by means of applying exclusively linear elements. Our attempt and main task will be, rather than further interpretation or developing of similar ideas, integrating of Daněk´s work into a wider natural scientific context. Doing this we would like to point out three sources and three parts of his geometrising visions: sources: • combinatorics and its visualisation (in historical sequence: Raimund Lullus Athanasius Kircher, S.J. … architecture of neural networks), • envelopes (in German: Einhüllenen, in Russian: ogibayushchie, in Czech: obálky) of curves, • light caustics (optical catastrophes), parts: • linear elements (segments) on a graph paper (predominantly pencil but sometimes coloured pencils and even felt-tip pens), • light effects, • simple rhythm (symmetry + dynamics) 1 Mundus combinatus “Father Kircher has studied all treatises on combinatorics, beginning with Lullus, and here you can see what he printed in his book Ars Magna Sciendi… »It resembles a crocheted cloth, « remarked Belbo. »Oh no, my dear, these are all possible combinations of n-elements. Total calculation, exactly as in Sefer Jecira. Calculation of combinations and permutations, the essence of Temura! «” Figure 1: Illustration from Kircher´s Ars Magna Sciendi Umberto Eco, the author of an armorial novel of post-modernism Foucault´s Pendulum (see [E1, p. 515]), supported this symptomatic passage by a contemporary engraving (see Figure 1) which he borrowed from a book on combinatorics by Athanasius Kircher, S.J. Ars Magna Sciendi published in Amsterdam in 1669. Kircher started with and consistently (sometimes almost absurdly) developed a method created by Raimund Lullus in his Ars Generalis Ultima from 1303 (sometimes also called Ars Magna et Ultima according to Strassbourg edition from 1598). The use of permutations, variations and combinations did not serve both men merely as a means for technical grasping of the problems (e.g. Figure 1 shows that the number of connecting lines equals the number of binomial variations with repetition of 18 elements, i.e. V (2,18) = 182 = 324 segments) but helped them, mainly during the process of “discovering”, – and somewhat ambitiously – to define possible scenarios. This way of thinking was typical for – not only exact – baroque sciences. More detailed information on this topic can be found in a beautiful monograph by Thomas Leinkauf Mundus combinatus [L] whose title became a symbolic subtitle of this chapter. The above-mentioned illustration is exactly the kind of example of an applied combinatorial scenario. Eighteen equidistantly arranged symbols are symmetrically doubled along the verticals with permissible relations (in our case every symbol with every other, including themselves) expressed simply by connecting the related symbols by a segment. The appropriate symbol is denoted by K18,18 in graph theory (see e.g. [H]). This mechanical procedure can be easily handled by a computer, however, the resulting visualisation lacks – in contrast with the copper engraving no. 1 – the aesthetic charge and lyrical excitedness (see Figure 2). Figure 2: Computer simulation of Figure 1 form. The impact of both Ars Magnas on further development of exact natural sciences was enormous. Under their influence, twenty year-old Gottfried Wilhelm Leibniz wrote Dissertatio de Arte Combinatorica, published in 1875-1890. However, as Eco points out in [E2, p. 243], while Lullus (as well as Kircher) consciously limited the number of terms and, for theological and rhetorical reasons, was ready to reject many of the combinations which would have possibly created inadmissible theorems, Leibniz is on the other hand intensely interested in creative logic through which he can, with the help of combinations, generate yet unknown worlds. “And to create an abstract model of all possible combinations is one thing, and the other one is to invent a machine which would perform these combinations completely. That is why Kircher himself as well as his disciple Schott threw themselves into devising mechanical spinning wheels, machines based on a kind of punch cards, computers ante litteram based on binary computation. In short, Kabbala applied on modern mechanics. ” This is how the introductory quotation goes on several lines further down (see again [E1, p. 515]. And indeed, if not yet from Kircher then surely from Leibniz, we are not so far from modern computers. At the present, one of the biggest hits of information technology is the concept of neural networks. At the same time we are to a certain degree witnessing a renaissance (in a new context) of the ideas of IT fathers Alan Turing, John von Neumann, Norbert Wiener and others. The analogy between structure and functioning of human brain and computers, or neural networks, is obvious. Some of the key concepts, such as bio-logic, multilayer perceptron (MLP), Hopfield’s net, etc. are treated for instance in Chapter 5 of [CH]. Book [MRS] represents an introduction to this topic. For our point of view it is essential that the architecture of neural networks shows similar outer signs as the above-mentioned combinatorial structures. Here the connection lines are led between interactive calculation elements – called neurons in neural networks terminology. Apart from countless applications (including strategical ones), the neural networks´ important advantage is their resistance to failure. Further possibilities of applied combinatorics – including simple visualisations – are discussed e.g. in [Kf]. Figure 3: Example of architecture of neural network Figure 4: Envelope generated by segments 2 Nonlinear structures Let us now consider a one-parameter set of curves (for example segments – see Figure 4) in the plane. The enveloping curve which is tangential to all these curves is called an envelope. At the same time, it is assumed that curves of the one-parameter class do not have singular points. More mathematically: If, on the set Ω × P ℝ2 × ℝ, where P ℝ is an interval, there is given a continuous function F(x,y,p) with continuous derivatives F/p, 2F/p2, where 2F/p 2 ≢ 0, then the curves defined by equation F(x,y,p) = 0 create a one-parameter system. If, for each value of parameter p P, a point is determined by equations F(x,y,p) = 0 a F/p = 0, then this point will be called characteristic or an extremal point of the system of curves generated by F(x,y,p) = 0. If furthermore it is possible to eliminate parameter p from the equations F(x,y,p) = 0 and F/p = 0 and if the related result is given by G(x,y) = 0 defining implicitly a curve, then this curve is called an enveloping curve (envelope) of system F(x,y,p) = 0. In every characteristic point [x0, y0, p0] Ω × P, for which 2F/p2 0, (and which is a regular point of the envelope curve), the enveloping curve touches a respective curve of the system. In other words: both curves have in such point a common tangent. A typical example of enveloping curve is a parametrically defined function x = - g'(p), y = - p g'(p) + g(p) which is a singular solution or singular integral of the well known Clairaut differential equation y = px + g(p), where p = dy/dx. This envelope is enveloped by lines given by general solution of the Clairaut equation (see e.g. [Km]). Quite analogously, it is possible to define an enveloping surface by one-parameter surface class defined by equation F(x,y,z,p) = 0. Figure 5: Orthonomic Figure 6: Anti-orthonomic Evolutes (envelopes of normals), caustics (will be treated in the sequel), orthonomics (see Figure 5), anti-ortonomics (see Figure 6) are examples of envelopes, together with seemingly much less mathematical objects such as the edge of conflagration in the fields or a crocheted cloth already mentioned in the foregoing part. For there are further (alternative, see e.g. [BG]) definitions of an envelope as a limit of intersection of neighbouring curves of one-parameter class or more comprehensibly as a boundary of an area filled with one-parameter class of curves. A whole monograph [Z] is devoted to the theory of envelopes. The generating curves of contours can be surprisingly also encountered within the framework of fractal theory (see [A], [AF]). However, here the generating curves are defined implicitly as invariant sets of the Hutchinson-Barnsley map generated by iterated functional systems (IFS). Invariant set does not mean that all its points are fixed, i.e. maps onto themselves, however, they will not escape a given set during iterations. Figure 7: Topological fractal An example of such invariant set is a topological fractal (see [AF]) in Figure 7 whose generating discrete dynamical system is of the form: 1(x,y) := (cos(x2/2 + y2/2), sin(x2/2 y2/2)), 2(x,y) := (1 cos(x2/2 + y2/2), sin(x2/2 y2/2)), 3(x,y) := (cos(x2/2 + y2/2), 1 sin(x2/2 y2/2)), 4(x,y) := (1 cos(x2/2 + y2/2), 1 sin(x2/2 y2/2)), The Hutchinson-Barnsley map is then simply defined as ℝ2. Thus if we denote the topological fractal from Figure 7 as ℱ, then it holds F(ℱ) = ℱ. For detection of the boundary of attractors of discrete dynamical systems and their basins of attraction, it is sometimes possible, with similar effect, to apply critical curves (see article [AD] in which the algorithms of software simulation are given a special attention). Further possibility is represented by plane mappings (two-dimensional projections) of multi-dimensional polytopes. Polytopes are geometrical objects bounded by portions of lines (in 2 dimensions), planes (in 3 dimensions) and hyperplanes (in 4 and more dimensions). Polytopes are called polygons and polyhedrons in two and three dimensions respectively. In 1981, Jonathan Bowen created a computer programme for projecting multi-dimensional cubes in the plane (see www.jpbowen.com/publications/ndcubes.html). Figure 8 shows a six-dimensional and Figure 9 a ten-dimensional cube. Figure 8: Six-dimensional cube Figure 9: Ten-dimensional cube H. S. M. Coxeter in his book [C] further generalised regular polytopes to regular complex polytopes in a similar way that complex numbers relate to real numbers. Figures 10 and 11 show that the knot points of generating segments of Coxeter´s regular complex polytopes are located on concentric circles. Figure 10: Coxeter´s polytope with Schläfli symbol {5/2,3,3} Figure 11: Coxeter´s polytope {5/2,3,5}, {5/2,5,5/2}, {3,5/2,5}, {3,3,5/2} The object in Figure 7 is – similarly as in Daněk´s drawings – structured. Here, the contours are created – opposite to segments exclusively used by Daněk (see also Figures 4, 6, 10, 11) or curves of just one type (e.g. circles in Figure 5) – by a whole variety of curves. Even though the generating curves were often – solely in the case of Daněk – segments (see Figures 4, 6, 10, 11), the generated structures (envelopes) are – with a single exception of two verticals in Figure 7 – non-linear. Similarly to Daněk´s work, the delicate effect of Figure 7 is reached by illusory simple rhythm originating from combination of symmetry and dynamics (irregularities) of envelopes (caustics). This topic is dealt with in detail in monograph [FG] illustrated with many beautiful pictures. 3 Let there be light! As mentioned in the previous part, a significant (physical) example of envelopes is represented by light caustics (a caustic originates e.g. when an illuminated ring is put on a pad, it can also be observed in a cup filled with tea). Let us imagine rays of light streaming simultaneously out of all points (I) in the direction of normals where : I ℝ2 is a planar curve with unit speed. Then (I) is called an originating wave front and the curve on which light is “formed” (it creates foci) is known as a caustic. Light foci originate where the infinitely close normals intersect – see Figure 12, where the caustic was formed after a beam of parallel rays reflected itself on a circle. Figure 12: Caustic Figure 13: Beam of optical catastrophes Since caustics are nothing else than light envelopes on which the intensity of light rises “in a jump”, we can also consider them in the framework of catastrophe theory (see [A], [AK]) created by René Thom, Vladimir I. Arnold and Eric C. Zeeman as elementary optical catastrophes. This idea comes from a University of Bristol Professor Michael V. Berry who simulated the optical catastrophes (with an unusual aesthetic result – see [B], [BU]) by diffracting laser beam on various types of surfaces. Figure 14: Optical catastrophe of the type “butterfly” We ourselves attempted a similar simulation by means of simply assembled optical systems for observation whose basis is comprised of lenses with suitable aberrations, an objective, a matrix and a shade (see [AK]). On the shade, we initially observed a beam cross-section of a sphere shape. When moving the lens along the optical axis, the diameter of the sphere fluctuated, and when moving it across the axis the image of the sphere turned in the same direction which evoked an impression of the whole sphere turning in space. When turning the lens towards the laser beam, a comatic cloud started forming around the point with interfering spots of light “trickling” from the sphere into the point and from the point into the cloud. We have gained very interesting caustic compositions from letting the the laser beam pass through worse defined environments like raindrops, bubbles, etc. The distances from the generating random means in which the individual cross-sections of the caustics were observed also proved essential. The whole procedure is described in detail and documented by five black-and-white photographs in the [AK] article. Figure 13 shows a whole range of optical catastrophes, Figure 14 shows a “butterfly” optical catastrophe. The cited works [B], [BU] contain include collections of superb photographs of caustics simulated in this way. The emphasis on the importance of light effects in Daněk´s work can be further supported by the fact that the motto of his Olomouc exhibition in Theatre of Music in 1990 was a quotation from Jakub Deml “The light is born as slowly as crystals”. Let us add that according to Deml´s friend Otokar Březina, “The light dies only in the resplendence of greater GREATER light.” References: [A] J. Andres: O nové přírodovědě a nutnosti nové přírodní filosofie. [On new natural science and a necessity of new natural philosophy]. Českoslov. časopis pro fyziku 46,1 (1996), 42-50. [AD] J. Andres and Z. David: Basin of attraction metamorphoses for two-dimensional endomorphisms. Acta Univ. Palacki. Olomouc, Fac. rer. nat., Phys. 35 (1996), 221-251. [AF] J. Andres and J. Fišer: Metric and topological multivalued fractals. Int. J. Bifurc. Chaos 14,4 (2004), 1277-1289. [AK] J. Andres a V. Křesálek: Katastrofy, chaos a krize v optice. [Catastrophes, chaos and crises in optics]. Jemná mechanika a optika 10 (1987), 307-310. [B] M.V. Berry: Singularities in waves and rays. In: „Physique des Défauts 25” (ed. R. Bahan et al.), North – Holland, Amsterdam, 1981. [BU] M.V. Berry and C. Uptstill: Morphology of caustics and their diffraction patterns. In: „Progress in Optics 18” (ed. E. Wolf), North – Holland, Amsterdam, 1980. [BG] J.W. Bruce and P.G. Giblin: Curves and Singularities. A Geometrical Introduction to Singularity Theory. Cambridge Univ. Press, Cambridge, 1984. [C] H. S. M. Coxeter: Regular Complex Polytopes. Cambridge Univ. Press, Cambridge, 1974; druhé vydání: 1991. [CH] P. Coveney and R. Highfield: Mezi chaosem a řádem. Hranice komplexity: hledání řádu v chaotickém světě. [Frontiers of Complexity: The Search for Order in a Chaotic World]. Mladá fronta, Praha, 2003. [E1] U. Eco: Foucaultovo kyvadlo. [Foucault’s Pendulum]. Odeon, Praha, 1991. [E2] U. Eco: Hledání dokonalého jazyka. [The Search for a Perfect Language]. Nakladatelství Lidové noviny, Praha, 2001. [FG] M. Field and M. Golubitsky: Symmetry in Chaos. A Search for Pattern in Mathematics, Art and Nature, Oxford University Press, Oxford, 1992. [H] F. Harary: Graph Theory. Addison-Wesley, Reading, 1969. [Kf] A. Kaufmann: Introduction a la combinatorique en vue des applications. Dunod, Paris, 1968. [Km] E. Kamke: Differentialgleichungen reeler Funktionen. Akad. Verlaggessellschaft Geest und Portig K.-G., Leipzig, 1952 [L] T. Leinkauf: Mundus combinatus. Studium zur Struktur der baroken Universalwissenshaft am Beispiel Athanasius Kircher SJ (1602-1680), Akademie Verlag, Berlin, 1993. [MRS] B. Müller, J. Reinhardt and M.T. Strickland: Neural Networks. An Introduction. Springer, Berlin, 1995. [Z] V. A. Zallgaller: Teoria ogibajuščich. [Theory of Envelopes]. Nauka, Moskva, 1975.
01.04.2004
Empfohlene Artikel
|
|||||||||||||
|
04.02.2020 10:17
Letošní 50. ročník Art Basel přilákal celkem 93 000 návštěvníků a sběratelů z 80 zemí světa. 290 prémiových galerií představilo umělecká díla od počátku 20. století až po současnost. Hlavní sektor přehlídky, tradičně v prvním patře výstavního prostoru, představil 232 předních galerií z celého světa nabízející umění nejvyšší kvality. Veletrh ukázal vzestupný trend prodeje prostřednictvím galerií jak soukromým sbírkám, tak i institucím. Kromě hlavního veletrhu stály za návštěvu i ty přidružené: Volta, Liste a Photo Basel, k tomu doprovodné programy a výstavy v místních institucích, které kvalitou daleko přesahují hranice města tj. Kunsthalle Basel, Kunstmuseum, Tinguely muzeum nebo Fondation Beyeler.
|









































 Potsdamer Str. 161 | Neu Divus in Zwitschermaschine, galerie und buchhandlug in Berlin! | Mit U2 nach Bülowstraße
Potsdamer Str. 161 | Neu Divus in Zwitschermaschine, galerie und buchhandlug in Berlin! | Mit U2 nach Bülowstraße
Kommentar
Der Artikel ist bisher nicht kommentiert wordenNeuen Kommentar einfügen